Итак. Т.к. я учусь и работник кафедры Информационной безопасности Одесского Национального Политехнического университета, хотелось бы Вам рассказать кое-что о криптографии.
Вкратце. Криптогра́фия (от греч. κρυπτός — скрытый и γράφω — пишу) — наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации. //Гласит нам Википедия
Давайте начнем с шифра Цезаря…
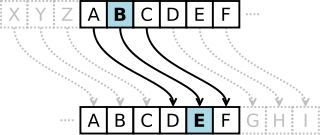
Шифр Цезаря — один из древнейших шифров. При шифровании каждый символ заменяется другим, отстоящим от него в алфавите на фиксированное число позиций. Шифр Цезаря можно классифицировать как шифр подстановки, при более узкой классификации — шифр простой замены.
Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки. Естественным развитием шифра Цезаря стал шифр Виженера. С точки зрения современного криптоанализа, шифр Цезаря не имеет приемлемой стойкости.
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами:
где — символ открытого текста, — символ шифрованного текста, — мощность алфавита, а — ключ.
С точки зрения математики шифр Цезаря является частным случаем аффинного шифра.
Можно заметить, что суперпозиция двух шифрований на ключах и — есть просто шифрование на ключе . Более общо, множество шифрующих преобразований шифра Цезаря образует группу
Примеры:
ЦЕЗАРЬ >>>>>5>>>>> ЫКМЕХБ
Шифр Полибия(тюремная азбука) – способ кодирования букв алфавита, с целью его приведения к виду, удобному для передачи по каналу связи (через стенку). Нередко в таблице использовался естественный порядок расположения букв алфавита, редуцированного до 28 букв, вписанных в сетку 5Х6.
Первоначально редким стуком в стену камеры указывалась строка, а затем через краткую паузу частым стуком, отсчитывалась буква. Например, для того, чтобы выстукать слово «кто» нужно дважды стукнуть редко, а затем пять раз ударить часто (буква К), затем четыре раза стукнуть редко и три часто (буква Т) и, наконец, трижды ударить редко и четыре раза часто (О). Принимающий стуки записывает одну за другой передаваемые буквы и, таким образом, составляет целые слова и фразы. Этот же принцип применяется при переговорах путем перемашки платком, причем строка указывается горизонтальной отмашкой, а счет букв – вертикальной.
Примеры:
ШИФРПОЛИБИЯ >>>>> >>>>>> ЮДЩБКЧГДВДУ
Самый распространенный “стиль” шифрования – Шифр Виженера(Бофора)
Шифр Виженера — метод полиалфавитного шифрования буквенного текста с использованием ключевого слова.
Этот метод является простой формой многоалфавитной замены. Шифр Виженера изобретался многократно. Впервые этот метод описал Джован Баттиста Беллазо (итал. Giovan Battista Bellaso) в книге La cifra del. Sig. Giovan Battista Bellasо в 1553 году, однако в XIX веке получил имя Блеза Виженера, швейцарского дипломата. Метод прост для понимания и реализации, он является недоступным для простых методов криптоанализа.
История
Первое точное документированное описание многоалфавитного шифра было сформулированно Леоном Баттиста Альберти в 1467 году, для переключения между алфавитами использовался металлический шифровальный диск. Система Альберти переключает алфавиты после нескольких зашифрованных слов. Позднее, в 1518 году, Иоганн Трисемус в своей работе «Полиграфия» изобрел tabula recta — центральный компонент шифра Виженера.
То, что сейчас известно под шифром Виженера, впервые описал Джованни Батиста Беллазо в своей книге La cifra del. Sig. Giovan Battista Bellasо. Он использовал идею tabula recta Трисемуса, но добавил ключ для переключения алфавитов шифра через каждую букву.
Блез Виженер представил своё описание простого, но стойкого шифра перед комиссией Генриха III во Франции в 1586 году, и позднее изобретение шифра было присвоено именно ему. Давид Кан в своей книге «Взломщики кодов» отозвался об этом осуждающе, написав, что история «проигнорировала важный факт и назвала шифр именем Виженера, несмотря на то, что он ничего не сделал для его создания».
Шифр Виженера имел репутацию исключительно стойкого к «ручному» взлому. Известный писатель и математик Чарльз Лютвидж Доджсон (Льюис Кэрролл) назвал шифр Виженера невзламываемым в своей статье «Алфавитный шифр» англ. The Alphabet Cipher, опубликованной в детском журнале в 1868 году. В 1917 году Scientific American также отозвался о шифре Виженера, как о неподдающемся взлому. Это представление было опровергнуто после того, как Казиски полностью взломал шифр в XIX веке, хотя известны случаи взлома этого шифра некоторыми опытными криптоаналитиками ещё в XVI веке.
Шифр Виженера достаточно прост для использования в полевых условиях, особенно если применяются шифровальные диски. Например, «конфедераты» использовали медный шифровальный диск для шифра Виженера в ходе Гражданской войны. Послания Конфедерации были далеки от секретных, и их противники регулярно взламывали сообщения. Во время войны командование Конфедерации полагалось на три ключевых словосочетания: «Manchester Bluff», «Complete Victory» и — так как война подходила к концу — «Come Retribution».
Гилберт Вернам попытался улучшить взломанный шифр (он получил название шифр Вернама-Виженера в 1918 году), но, несмотря на его усовершенствования, шифр так и остался уязвимым к криптоанализу. Однако работа Вернама в конечном итоге всё же привела к получению шифра, который по-настоящему трудно взломать.
Описание
В шифре Цезаря каждая буква алфавита сдвигается на несколько позиций; например в шифре Цезаря при сдвиге +3, A стало бы D, B стало бы E и так далее. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая tabula recta или квадрат (таблица) Виженера. Применительно к латинскому алфавиту таблица Виженера составляется из строк по 26 символов, причём каждая следующая строка сдвигается на несколько позиций. Таким образом, в таблице получается 26 различных шифров Цезаря. На разных этапах кодировки шифр Виженера использует различные алфавиты из этой таблицы. На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от символа ключевого слова. Например, предположим, что исходный текст имеет вид:
ATTACKATDAWN
Человек, посылающий сообщение, записывает ключевое слово («LEMON») циклически до тех пор, пока его длина не будет соответствовать длине исходного текста:
LEMONLEMONLE
Первый символ исходного текста A зашифрован последовательностью L, которая является первым символом ключа. Первый символ L шифрованного текста находится на пересечении строки L и столбца A в таблице Виженера. Точно так же для второго символа исходного текста используется второй символ ключа; то есть второй символ шифрованного текста X получается на пересечении строки E и столбца T. Остальная часть исходного текста шифруется подобным способом.
Исходный текст: ATTACKATDAWN
Ключ: LEMONLEMONLE
Зашифрованный текст: LXFOPVEFRNHR
Расшифрование производится следующим образом: находим в таблице Виженера строку, соответствующую первому символу ключевого слова; в данной строке находим первый символ зашифрованного текста. Столбец, в котором находится данный символ, соответствует первому символу исходного текста. Следующие символы зашифрованного текста расшифровываются подобным образом.
Если буквы A-Z соответствуют числам 0-25, то шифрование Виженера можно записать в виде формулы:
Расшифровка:
Криптоанализ
Шифр Виженера «размывает» характеристики частот появления символов в тексте, но некоторые особенности появления символов в тексте остаются. Главный недостаток шифра Виженера состоит в том, что его ключ повторяется. Поэтому простой криптоанализ шифра может быть построен в два этапа:
Поиск длины ключа. Можно анализировать распределение частот в зашифрованном тексте с различным прореживанием. То есть брать текст, включающий каждую 2-ю букву зашифрованного текста, потом каждую 3-ю и т. д. Как только распределение частот букв будет сильно отличаться от равномерного (например, по энтропии), то можно говорить о найденной длине ключа.
Криптоанализ. Совокупность l шифров Цезаря (где l — найденная длина ключа), которые по отдельности легко взламываются.
Тесты Фридмана и Казиски могут помочь определить длину ключа.
Метод Касиски
В 1863 году Фридрих Касиски был первым, кто опубликовал успешный алгоритм атаки на шифр Виженера, хотя Чарльз Беббидж разработал этот алгоритм уже в 1854 году. В то время когда Беббидж занимался взломом шифра Виженера, John Hall Brock Thwaites представил новый шифр в «Journal of the Society of the Arts»; когда Беббидж показал, что шифр Thwaites’а является лишь частным случаем шифра Виженера, Thwaites предложил ему его взломать. Беббидж расшифровал текст, который оказался поэмой «The Vision of Sin» Альфреда Теннисона, зашифрованной ключевым словом Emily — именем жены поэта.
Тест Касиски опирается на то, что некоторые слова, такие как «the» могут быть зашифрованы одинаковыми символами, что приводит к повторению групп символов в зашифрованном тексте. Например: сообщение, зашифрованное ключом ABCDEF , не всегда одинаково зашифрует слово «crypto»:
Ключ: ABCDEF AB CDEFA BCD EFABCDEFABCD
Исходный текст: CRYPTO IS SHORT FOR CRYPTOGRAPHY
Шифрованный текст: CSASXT IT UKSWT GQU GWYQVRKWAQJB
Зашифрованный текст в данном случае не будет повторять последовательности символов, которые соответствуют повторным последовательностям исходного текста. В данном шифрованном тексте есть несколько повторяющихся сегментов, которые позволяют криптоаналитику найти длину ключа:
Ключ: ABCDAB CD ABCDA BCD ABCDABCDABCD
Исходный текст: CRYPTO IS SHORT FOR CRYPTOGRAPHY
Шифрованный текст: CSASTP KV SIQUT GQU CSASTPIUAQJB
Более длинные сообщения делают тест более точным, так как они включают в себя больше повторяющихся сегментов зашифрованного текста. В данном шифрованном тексте есть несколько повторяющихся сегментов, которые позволяют криптоаналитику найти длину ключа:
Шифрованный текст: DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
Расстояние между повторяющимися DYDUXRMH равно 18, это позволяет сделать вывод, что длина ключа равна одному из значений: 18,9,6,3 или 2. Расстояние между повторяющимися NQD равно 20. Из этого следует, что длина ключа равна 20 или 10, или 5, или 4 или 2. Сравнивая возможные длины ключей, можно сделать вывод, что длина ключа (почти наверняка) равна 2.
Тест Фридмана
Тест Фридмана (иногда называемый каппа-тест) был изобретен Вильямом Фридманом в 1920 году. Фридман использовал индекс совпадения, который измеряет частоты повторения символов, чтобы взломать шифр. Зная вероятность κr того, что два случайно выбранных символа текста совпадают (примерно 0,067 для англ. языка) и вероятность совпадения двух случайно выбранных символов алфавита (примерно 0,0385 для англ. языка), можно оценить длину ключа как:
Из наблюдения за частотой совпадения следует:
Где С — размер алфавита (26 символов для англ. языка), N — длина текста, и n1 до nc — наблюдаемые частоты повторения символов зашифрованного текста. Однако, это только приблизительное значение, точность которого увеличивается при большем размере текста. На практике это было бы необходимо для перебора различных ключей приближаясь к исходному.
Частотный анализ
Как только длина ключа становится известной, зашифрованный текст можно записать во множество столбцов, каждый из которых соответствует одному символу ключа. Каждый столбец состоит из исходного текста, который зашифрован шифром Цезаря; ключ к шифру Цезаря является всего-навсего одним символом ключа для шифра Виженера, который используется в этом столбце. Используя методы, подобные методам взлома шифра Цезаря, можно расшифровать зашифрованный текст. Усовершенствование теста Казиски, известное как метод Кирхгофа, заключается в сравнении частоты появления символов в столбцах с частотой появления символов в исходном тексте для нахождения ключевого символа для этого столбца. Когда все символы ключа известны, криптоаналитик может легко расшифровать шифрованный текст, получив исходный текст. Метод Кирхгофа не применим, когда таблица Виженера скремблирована, вместо использования обычной алфавитной последовательности, хотя тест Касиски и тесты совпадения всё ещё могут использоваться для определения длины ключа для этого случая.
Примеры:
ШИФРБОФОРА >>>>>КЛЮЧ>>>>> ВУТЗЛЩТЕЪЛ
На этом я закончу, но помните, что есть ещё много способов и типов крипто-шифрования такие, как: Play Fair, Двойной квадрат, Шифр Гронсфельда, Гомоморфная подстановка и пр.
Добавить комментарий